
ExploreLearning Gizmo: Translating and Scaling Functions (already downloaded on computer).

Graphmatica (already downloaded on computer).Materials List and Advanced Preparations: (C) use properties of functions to analyze and solve problems and make predictions (A) use functions such as logari\thmic, exponential, trigonometric, polynomial, etc. (3) The student uses functions and their properties to model and solve real-life problems. x), |f(x)|, f(|x|), to the parent functions.(A) apply basic transformations, including a (2) The student interprets the meaning of the symbolic representations of functions and operations on functions within a context. (D) recognize and use connections among significant points of a function (roots, maximum points, and minimum points), the graph of a function, and the symbolic representation of a function and (B) determine the domain and range of functions using graphs, tables, and symbols

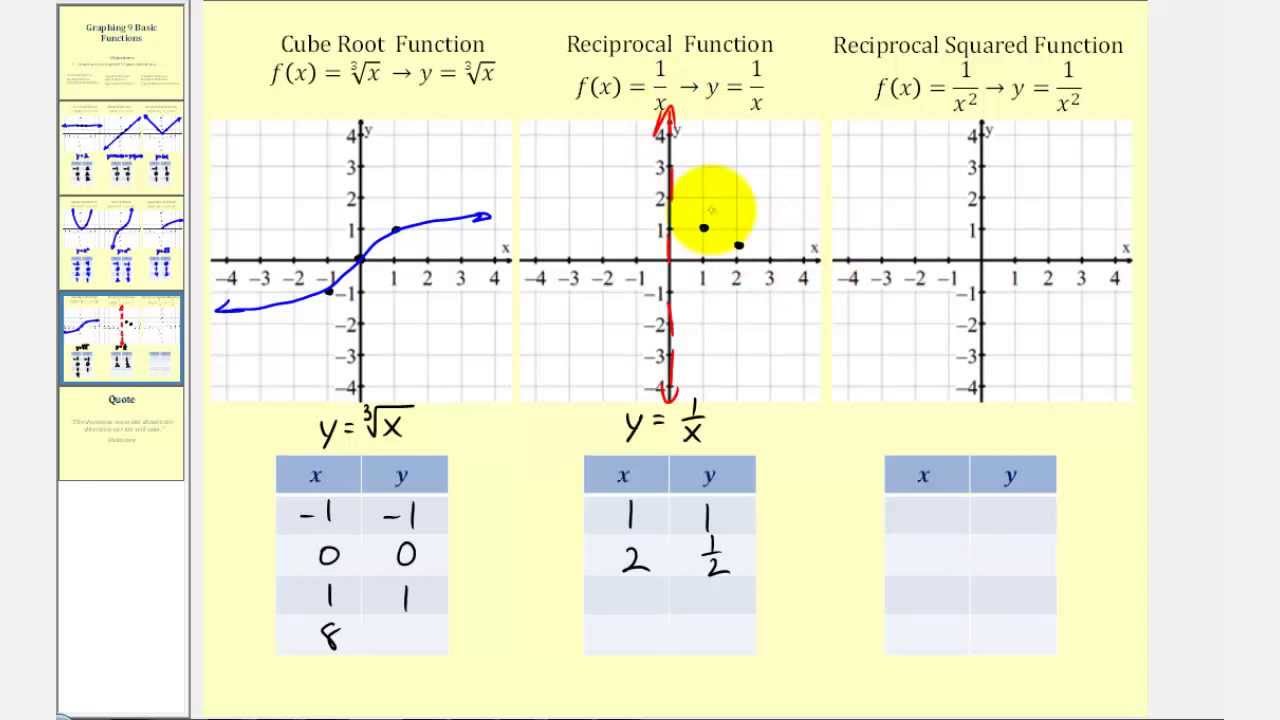
(A) describe parent functions symbolically and graphically, including y = x n, y = ln x, y = log a x, y =, y = e x, y = a x, y = sin x, etc. (1) The student defines functions, describes characteristics of functions, and translates among verbal, numerical, graphical, and symbolic representations of functions, including polynomial, rational, radical, exponential, logari\thmic, trigonometric, and piecewise-defined functions. Students use a variety of representations (concrete, numerical, algori\thmic, graphical), tools, and technology to model functions and equations and solve real-life problems. Students also use functions as well as symbolic reasoning to represent and connect ideas in geometry, probability, statistics, trigonometry, and calculus and to model physical situations. Students use functions, equations, and limits as useful tools for expressing generalizations and as means for analyzing and understanding a broad variety of mathematical relationships. Students use symbolic reasoning and analytical methods to represent mathematical situations, to express generalizations, and to study mathematical concepts and the relationships among them. (1) In Precalculus, students continue to build on the K-8, Algebra I, Algebra II, and Geometry foundations as they expand their understanding through other mathematical experiences.
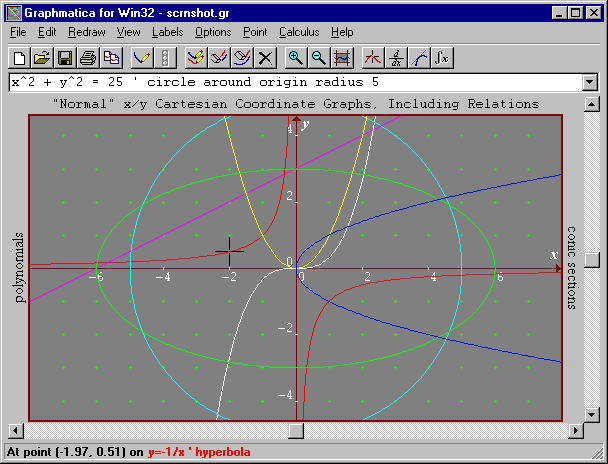
Functions graphmatica how to#
Through this activity, students will also gain an understanding of mathematics as a tool to describe the world in which we live.ġ) recognize different types of functions that can be used to describe real-worldĢ) formulate equations of functions that best describe particular relationshipsģ) apply their knowledge of how to manipulate functions in order to create images of these real-world objectsĤ) develop connections between mathematics and the real-world. Their experience with the manipulation of functions, along with this increased repertoire of functions, will give the students the freedom to more accurately recreate images that are less contrived. By having an expanded awareness of various types of functions, they will be able to more easily see how functions can be used to represent particular images. Concepts: Students will be able to recognize shapes, designs, and structures existing around them in terms of functions.


 0 kommentar(er)
0 kommentar(er)
